목차
오차역전파
경사하강
활성함수
최적화 함수
초기 가중치 설정함수
배치 정규화
이전 장에서 입력노드가 출력노드에 미치는 영향력/weight를 기울기라고 표현했다.
경사하강법을 다르게 표현하면, 기울기 감소법이라고 할 수 있겠다.
이게 뭔 소리람? 기울기를 기울기 감소시켜?
지금부터
입력노드의 영향력을 가리키는 기울기를 weight라 표현하고,
경사하강법에서 가리키는 기울기를 gradient라 표현하겠다.
통계학자들이나 컴공학자들이나 Solution을 찾는 문제를
Convex function형태로 만들려고 한다. 왜?
"우리가 이미 알고 있는 함수의 성질을 사용하면 Solution을 찾는 방법을 빠르게 찾을 수 있으니까"
"알고 있다는 이유 이외에도 Convex function의 Solution을 찾는 수치적/컴퓨팅적 방법이 간단/효율적이기 때문이다"
그런 이유로 Target 확률분포과 대비해
우리가 만든 모델이 얼마나 정확한지(부족한지) 측정하려고 정의한 손실함수를 Convex function꼴로 만들어 사용한다.
사전설명이 길었다.
어째든 손실함수가 아래 볼록이라면, 기울기(미분값)가 0일 때, 최소값을 갖는다.
해당 최소값이 지역 최소값일수도 있고 안장점일 수도 있고, 전역 최소값일 수도 있지만, 일단은 전역 최소값이라 하겠다.
어떻게 하면 최소값을 효율적으로 찾을 수 있을까?
이에 대한 해답이 경사하강법Gradient Descent Method다.
경사하강법이란?
노드의 weight를 손실함수에 대한 weight의 편미분값(gradient)만큼 감소(수정)시키는 최적화방법.
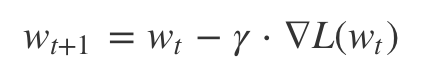
수정 횟수를 반복하면
1회 학습/수정한 것보다 n회 학습/수정한 것이
더 정확한 weight를 찾는데 도움이 되지 않을까?
--> 응! 당연하지
그래서 경사하강법은 최적값을 찾을 때까지 여러번 반복할 수 있다는 장점이 있다.
경사하강법을 여러번 반복한다면 "같은 데이터를 반복해서 사용할 수 있다는 의미"다.
여기서 같은 데이터를 여러번 사용해도 되는 이유? (= learning rate를 사용하는 이유)
weight를 조절할 때, gradient 만큼 한꺼번에 조절하지 않고,
learning rate(alpha)만큼 조금씩 반영하면서 줄여 나가기 때문이다.
너무 한꺼번에 gradient를 반영해서 감소시키면, 무한 발산하면서 최소값에 도달할 수 없기 때문이다.
반복해서 학습하면서 weight 를 조절하면서 손실함수를 최소화하는 과정이 아래의 그림이다.
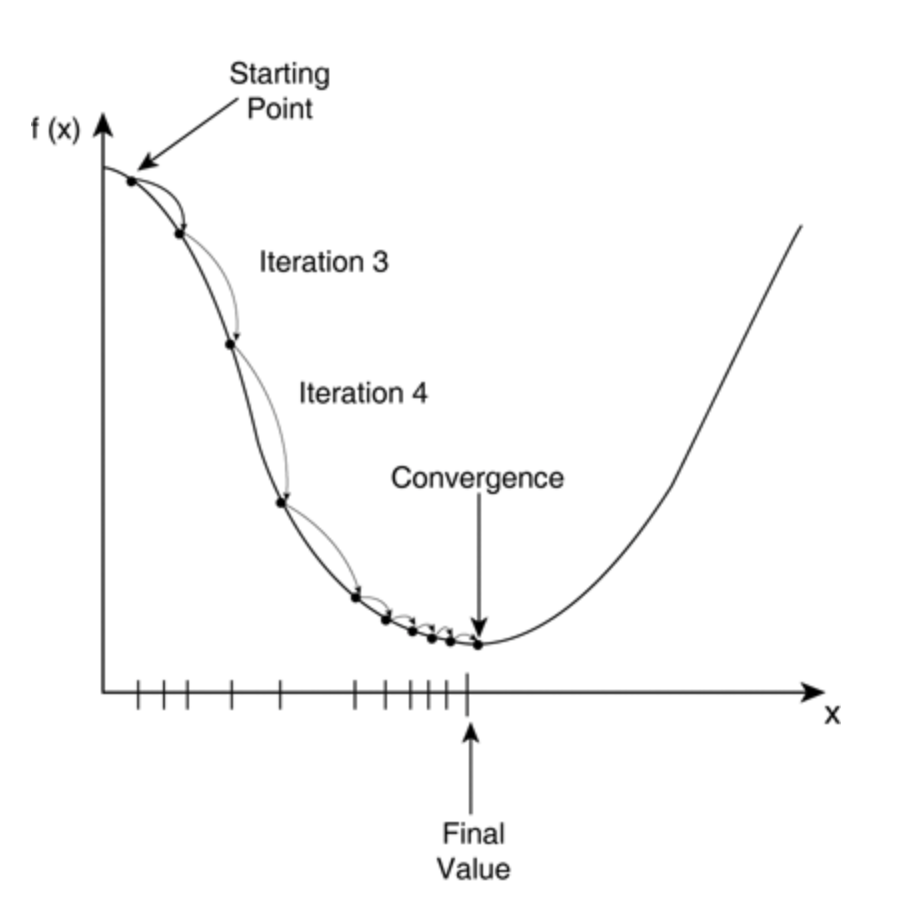
경사하강법의 종류 : 연산처리 방식 기준
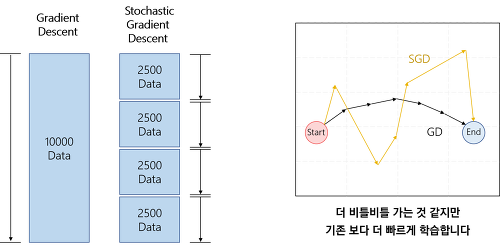
1. 배치 경사하강법 : 모든 데이터를 한꺼번에 사용해서 손실함수값을 계산하고 weight 조절하기를 n번 반복함
2. 확률 경사하강법 : 데이터를 랜덤하게 섞고, 하나씩 사용해서 손실함수값을 계산하고, weight조절하고, 데이터를 다 쓰면 다시 반복
3. 미니배치 경사하강법 : *****가장 많이 사용하는 방법 / 확률 경사하강법과 동일한 용어로 사용됨.******
- 데이터를 막 섞는다.
- 여러개 그룹으로 나눈다.
- 각 그룹마다 손실함수값을 계산하고 weight 조절한다.
- 모든 그룹을 다 사용하면 다시 반복한다.
*병렬처리가 가능하다 == GPU를 적용할 수 있다
* 용어정리
: mini-batch의 개수(iteration) X mini-batch의 크기(size: 32, 64, 128) = data 크기(개수)
: 데이터를 반복해서 사용하는 횟수(epoch)
경사하강법의 종류 : 최적화 방식 기준
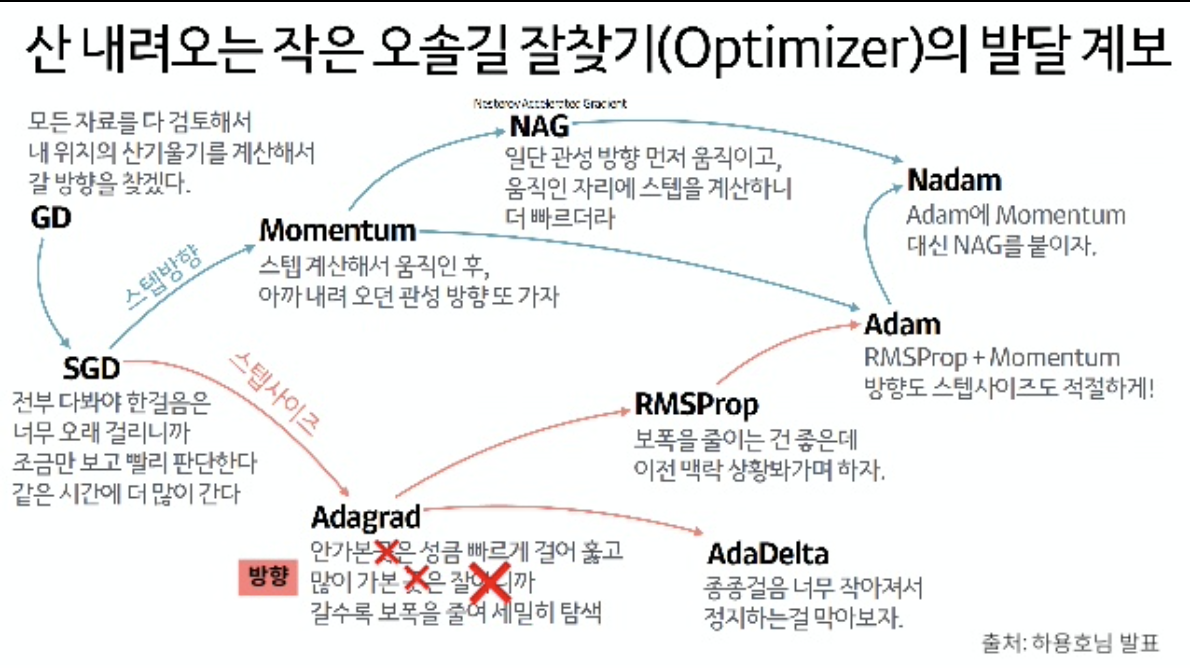
기본이 되는 (Stochastic) Gradient Descent 방식에 여러가지 파생되는 버전이 존재한다.
최적값에 도달하지 못하는 문제를 ㄱㅐ선하고자 등장함.
안장점/지역최소값에 도달하지 않도록 더많이 움직이게, 더 적게 움직이게 하는 방식이 추가되어 만든 최적화 함수들.
1. Momentum/ Nesterov Momentum : 특정 방향으로 자주 update가 이루어진다면, 그 방향에 velocity가 생겨서 더 많이 이동함.
2. Adagrad : 많이 갔던 방향에 대해 그 영향력을 점점 줄여나가는 방식 ; minima에 가까워지면서 느려져야 하기 때문
3. RMSProp(Root Mean Squared Prop) : 과거 이동방향에 대한 영향력을 줄이는 방식에 비율을 추가함.
4. Adam = Adagrad + Momentum
출처 :
'DataMining > Deeplearning' 카테고리의 다른 글
| DL - 기초; 배치 정규화 (0) | 2021.02.27 |
|---|---|
| DL - 기초; 초기화 (0) | 2021.02.27 |
| DL - 기초; 신경망소개/CNN/RNN (0) | 2021.02.27 |
| DL - 기초; 활성함수 (0) | 2021.02.27 |
| DL - 기초 ; 오차역전파 (0) | 2021.02.27 |

